회귀(Regression)
- 시초: 19C 통계학자 프랜시스 골턴Francis Galton, 키가 큰 사람의 아이가 부모보다 더 크지 않다는 사실을 관찰하고, "평균으로 회귀한다"는 표현을 사용
- 데이터의 값은 평균과 같은 기존의 경향으로 돌아가려는 경향이 있다는 것
- 여러 변수들 간의 상관 관계를 파악하여 어떤 특정 변수의 값을 다른 변수들의 값을 이용하여 설명, 예측하는 수리식을 찾는 방법
- 회귀식을 찾는 것
회귀분석의 유형
- 변수의 개수 및 계수의 형태에 따라 구분한다
- 독립 변수의 개수에 따라
- 단순회귀분석: 독립변수가 1개인 경우, 단일 회귀분석이라고도 함.
- 다중회귀분석: 독립변수가 여러 개인 경우
- 회귀 계수의 형태에 따라
- 선형: 계수를 선형 결합으로 표현할 수 있는 경우
- 비선형: 계수를 선형 결합으로 표현할 수 없는 경우
- 종속 변수의 개수에 따라
- 단변량univariate 회귀모델 : 종속변수가 1개인 경우
- 다변량multivaiate 회귀모델 : 종속변수가 여러 개인 경우
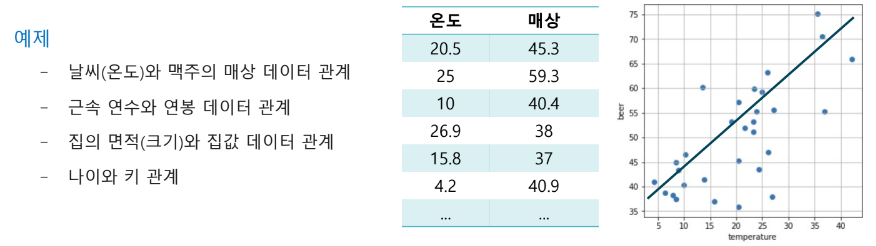
회귀식 예시
단순회귀분석
y = 3x + 1
- y 종속변수
- x 독립변수
- 3 계수(coefficient)
- 1 절편(intercept)
다중회귀분석
y = 100X1 + 200X2 + 300X3 + 400X4
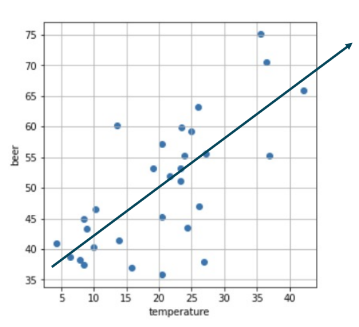
선형회귀
- 종속 변수가 독립 변수와 회귀 계수의 선형 조합으로 표현 가능한 경우
- 파라미터(계수)에 대한 선형성만을 가정함
- 독립변수, X와 종속 변수, y간의 상호 연관성 정도를 파악하기 위한 분석 기법
- 하나의 변수가 변함에 따라 대응되는 변수가 어떻게 변하는지를 측정하는 것
- 변수 간의 인과관계를 분석할 때 많이 사용
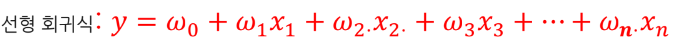
단순선형회귀(Simple Linear Regression)
- 데이터의 분포를 직선으로 가정하고 데이터를 학습해서 예측
- 독립변수가 1개이고, 종속변수도 1개
- 독립변수와 종속변수 간의 관계를 선형적으로 파악하는 회귀 방식
- 회귀계수 : 독립변수가 종속변수에 끼치는 영향력(설명력)의 정도로써, 직선의 기울기(slope)
- 절편 : 독립변수가 0일 때 상수값
- 직선이 데이터에 부합하려면, 적합한 회귀계수와 절편을 찾아야한다.
오차와 손실함수(Cost Function)
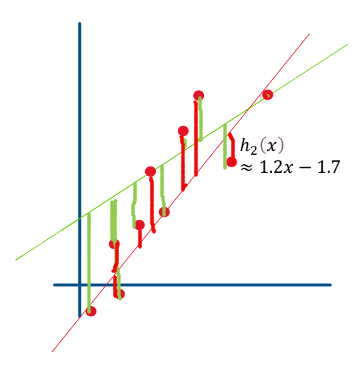
회귀식이 각 값 별로 적용되는 오차의 합으로 어떤 회귀식이 더 좋은지 판별한다.
오차식

오차의 합을 가장 적게 만드는 회귀식을 찾기 위해 회귀식을 사용한다.
잔차 제곱 오차함수
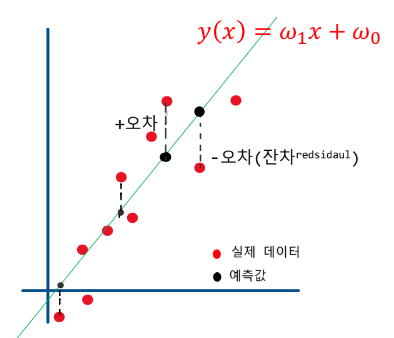
- 잔차(residual), 오차(error) : 통계학적으로 모집단, 표본집단에 의해 용어가 다르나 이 파트에선 혼재해서 사용
- 실제 값과 회귀 모델식에 의해 계산한 추정값(점추정치)의 차이
- 잔차 값의 작을수록, 구해진 회귀식이 데이터를 잘 설명하고 있다고 볼 수 있다.
- xn에서의 오차(점추정치)
- 잔차 제곱합(RSS : Resiual sum of Squares)
- 모든 데이터 점의 잔차를 제곱하여 합한 것
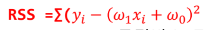
- xi : 독립변수 집합 X의 원소
- yi : 종속변수 집합 Y의 원소
- 손실함수(loss function) / 비용함수(cost function)
- 회귀 계수를 추정할 때 손실을 최소화할 목적으로 사용하는 함수
- 직선 모델이 "데이터에 부합"하려면?
- 가장 적은 오류를 발생시키는 직선을 찾음
- 손실함수 값이 최소가 되는 회귀모형을 만듬
회귀분석 손실함수(Cost Function)

회귀 계수 탐색
- 최소제곱법(OLS)
- 경사하강법(수치해적 방법)
- 임의의 숫자를 난수로 발생시킨 후, 계속해서 조금씩 변화시키면서 w1, w0의 값을 넣다가 cost가 최소 값이 됐을 때, 해당 값이 최소가 되는 값을 찾는다.

최소제곱법/정규방정식
sklearn.linear_model.LinearRegression 활용하면 회귀계수와 절편을 반환한다.
sklearn 공식문서 LinearRegression
정리
- 최적의 회귀 모형을 만든 다는 것 : 손실함수(비용함수)인 MSE 값이 최소가 되는 회귀계수(W1.W0)을 찾는 것
- 수치해적 방법 : 경사하강법(반복적인 계산에 의해 근사값을 구하는 수치 계산법) -> 딥러닝을 만든 방법
- 해석학적 방법(최소제곱법:OLSOrdinary Least Sqaures)
- 직선 모델의 경우 근사값이 아니라 정규방정식Normal Equation이라는 닫힌 형태의 계산식을 직접 풀어 정확한 해를 구하는 방법(Ax=B, ATAx = ATB) – 가우스/르장드르
- 반복계산이 아니라 1회의 계산으로 최적의 W를 구할 수 있다.
- 계산 시간이 빠르고 정확한 답을 제공한다
- 문제의 본질을 잘 이해할 수 있고, 다차원 데이터에 대응하며 곡선모델로 확장하기 좋다
- w0와 w1으로 손실 함수(단순선형회귀)를 각각 편미분한 값이 0이 되는 연립방정식의 해를 구한다.
- 특성의 개수(입력의 차원)가 많을수록 느려지고 다양한 문제에 적용할 수 없다
결정계수(Coefficint of Determinant)
개체(종속변수)가 가지는 총 변량 중 회귀식이 설명(차지)하는 변량의 비율
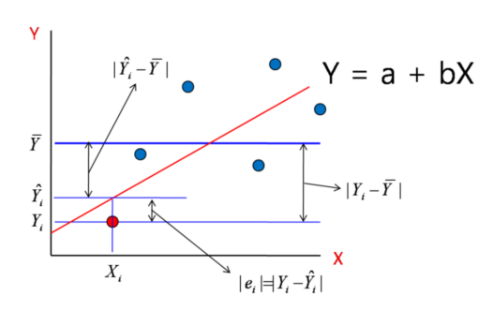
- 모델이 얼마나 종속 변수를 잘 설명하는가에 관한 지표
- 만약 모델의 잔차가 매우 큰 경우 결정계수는 마이너스가 나올 수 있다
- 최소제곱법을 이용한 선형 회귀에서는 예측값과 실제값의 상관 계수를 제곱한 수치가 결정 계수와 같아진다.(0 ≤ R2 ≤ 1)
- 결정계수 해석
- 결정 계수의 값은 0 <= R2 <= 1이며, 1에 가까울수록 설명력이 강하고 0에 가까울수록 설명력이 약하다
sklearn.metrics.r2_score
sklearn 공식문서 r2 score
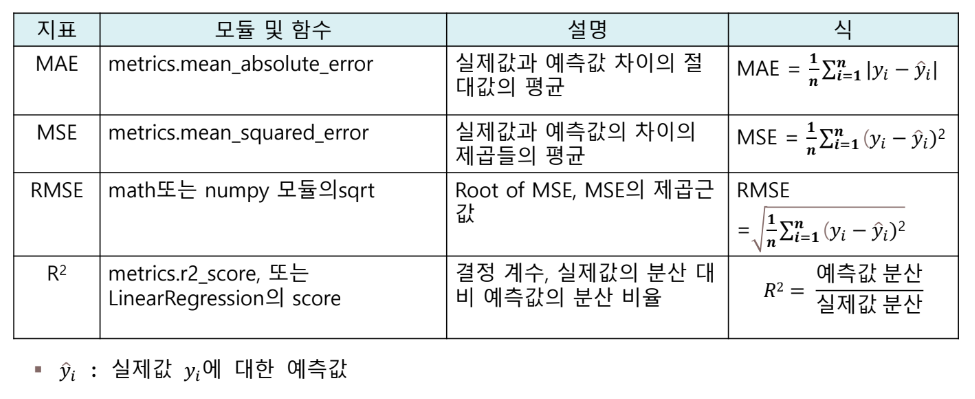
선형회귀 이론 정리
- 머신 러닝의 개념으로 해석하는 선형회귀
- 가설함수 : 최적의 회귀선
- 손실함수 : 예측값과 실제값과의 차이(오차)의 합(평균)
- 회귀 모델 평가 지표
- 모델 성능 평가
'머신러닝 및 딥러닝 > 머신러닝' 카테고리의 다른 글
| 머신러닝 모델 최적화 - 과적합 (0) | 2023.02.08 |
|---|---|
| 다항회귀이론( + 사이킷런 transformer) (0) | 2023.02.08 |
| 경사하강법 이론2(+ Feature Scaling) (0) | 2023.02.08 |
| 경사하강법 이론 (0) | 2023.02.08 |
| 다중선형회귀 이론 (0) | 2023.02.07 |
