경사하강법
여러 종류의 문제에서 최적의 해법을 찾을 수 있는 일반적인 최적화(Optimization) 알고리즘
- 손실(비용) 함수를 최소화 하기위해 반복해서 파라미터를 조정하는 것
- 선형 회귀의 경우 손실함수(MSE(평균오차제곱))을 최소화하는 파라미터 W1, W0에 대해 함수의 현재 기울기(그래디언트)를 계산한 후 기울기가 감소하는 방향으로 진행하고, 기울기가 0이 되면 최솟값에 도달한 것
- 비유 : 앞이 보이지 않는 안개가 낀 산을 내려올 때는 모든 방향으로 산을 더듬어 가면서 산의 높이가 가장 낮아지는 방향으로 한발 씩 내딛어 내려올 수 있다.
경사하강법의 장점
- 함수가 너무 복잡해 미분 계수를 구하기 어려운 경우
- 경사하강법을 구현하는게 미분 계수를 구하는 것보다 더 쉬운 경우
- 데이터 양이 너무 많아 효율적인 계산이 필요한 경우
- '데이터를 기반으로 알고리즘이 스스로 학습한다'는 머신러닝의 개념을 가능하게 해준 핵심 기법 중 하나
학습률(Learning Descent)
- 매 계산(stp)마다 적용되는 이동 거리
- 기울기 갱신의 폭 결정
- 하이퍼파라미터로 조절 가능함
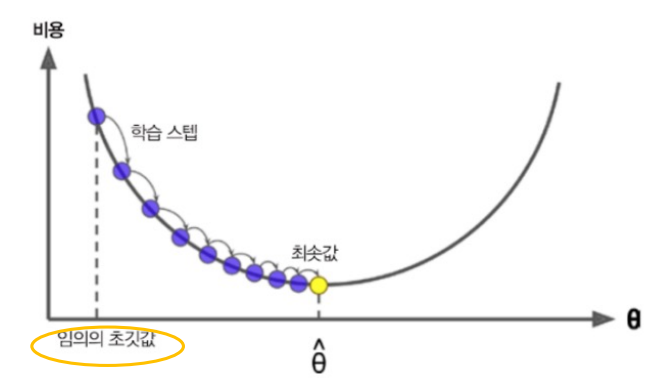
- 각 경사마다 미분을 통해 기울기 계산
- 기울기를 wi 값에 빼면 기울기가 음수 일 때는 왼쪽으로, 기울기가 양수 일 때는 오른쪽으로 점차 이동
- 결국 손실함수가 최저가 되는 점에 도달
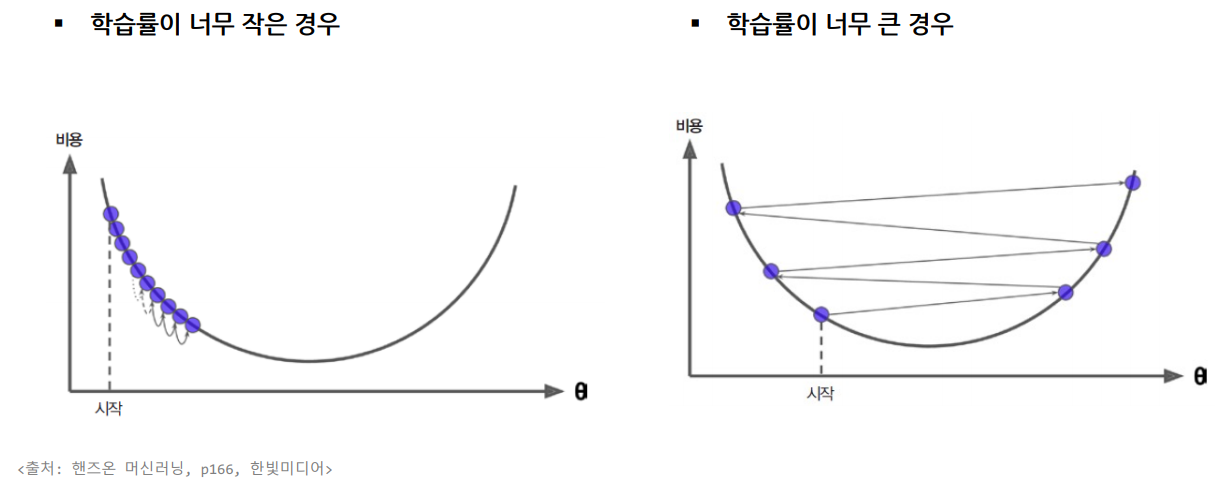
- 학습률이 너무 작은 경우 : 최솟값에 수렴하지 못한다
- 학습률이 너무 큰 경우 : 모델이 발산한다
경사하강 코드 구현
- 기울기가 충분히 작아질 때까지 갱신하다가 기울기(𝜃)가 평평한 곳에 도달하면 갱신을 종료한다.
- 기울기 갱신 횟수, 기울기 최솟값을 사전에 지정(하이퍼파라미터)
경사하강법 유의점
모든 손실함수가 볼록함수가 아니며, 비볼록 함수일 경우 최적값(global optimum)을 찾지못하고, 지역 최적값(local optimum)을 구하게 될 수도 있음.
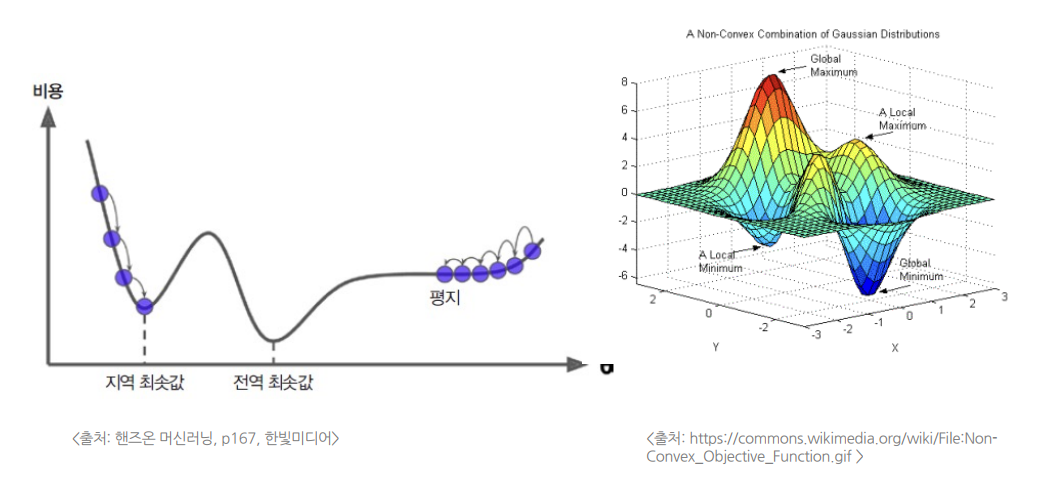
- 선형회귀의 MSE 손실함수는 반드시 볼록함수이다.
- 지역 최솟값이 없고, 하나의 전역 최솟값만 잇다.
- 연속된 함수이고 기울기가 갑자기 변하지 않는다.
- 경사하강법을 통해 전역 최솟값에 도달할 수 있다.
경사하강법과 최소제곱법의 차이
- 경사 하강법과 최소 제곱법 모두 예측 알고리즘에 해당한다.
- 경사 하강법이 수학적 최적화 알고리즘으로서 적절한 학습비율(learningrate)를 설정해야 하고 많은 연산량이 필요하지만 정규방정식에는 그와 같은 단점이 없다는 장점이 있다.
- 정규방정식은 행렬 연산에 기반하기 때문에 특성의 개수가 엄청나게 많을 경우 연산이 느려지는 것을 피할 수 없다.
- 경사 하강법은 아무리 많은 특성이 존재하더라도 일정한 시간 내에 해법을 찾는 것이 가능하다.
- 그러므로 예측 알고리즘을 선택할 때 있어 특성의 개수에 따라 알맞은 것을 선택하여야 한다.
배치(batch)와 에폭(epoch)
배치
- 1회의 경사 업데이트(스텝)에 사용되는 데이터 집합
- 이 때 사용되는 데이터 집합의 개수를 배치 크기(배치 사이즈)라고 함
- 예) 전체 데이터 세트 : 100개, 배치 사이즈 20
- 배치 개수 : 5, 경사(기울기) 업데이트 수 : 5회
에폭
- 전체 데이터들을 한번 모두 사용하는 것
- 일반적으로 경사하강법은 수십, 수백번 이상 에폭을 수행
- 예) 전체 데이터 세트 : 100개, 배치 사이즈 : 20, 에폭 : 1000
- 에폭 1회 -> 배치 개수 : 5, 경사(기울기) 업데이트 수 : 5회
- 에폭 1000회 -> 경사 업데이트 수(학습 횟수) : 5000
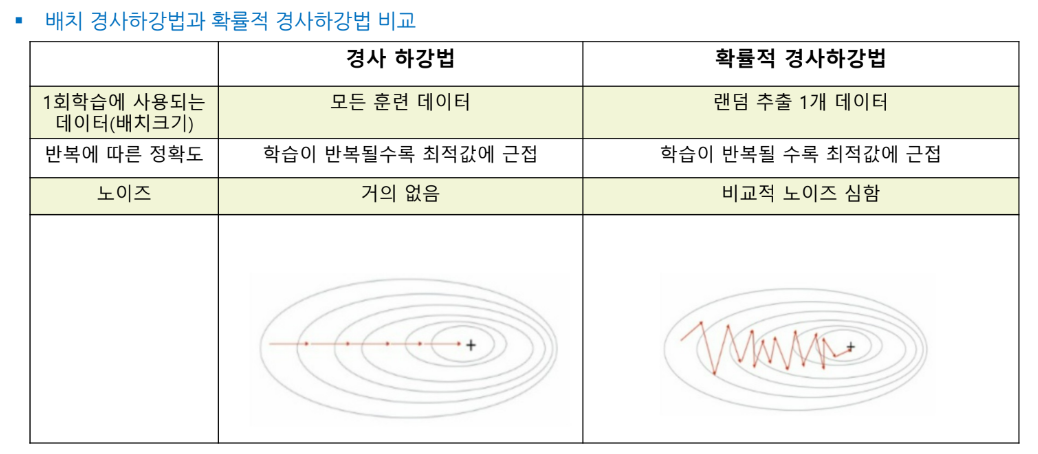
배치 경사하강법(batch gradient descent)(full gradient descent)
- 매 스텝(1회의 기울기 갱신, 가중치 갱신)에서 훈련 데이터 전체를 사용(배치의 크기:훈련 데이터 전부)하여 계산한 후 최적의 한 스텝을 나아감.(Full gradient descent)
- 매우 큰 훈련 세트에서는 아주 느림
- 한 개의 배치에 전체 학습 데이터가 모두 들어간다
확률적 배치 경사하강법(SGD:stochastic gradient descent)
- 매 스텝에서 한 개의 샘플(훈련 데이터)을 무작위로 선택하고 그 하나의 샘플에 대한 그래디언트(기울기)를 계산함
- 한 개의 배치에 임의의 학습 데이터 1개만 들어간다
- 매 스텝에서 다루어야 할 데이터가 매우 작으므로(배치의 크기 1) 처리 속도가 빠름
- 빠르게 최적점을 찾을 수 있지만 정확도는 낮아짐
- 매우 큰 훈련 데이터도 학습 가능함
- 데이터가 들어오는 즉시 가중치를 갱신할 수 있어 온라인 학습이 가능하며 즉각적인 시스템 대응이 가능
미니 배치 경사하강법
- 확률적 경사하강법 및 배치 경사하강법의 절충안
- 각 스탭에서 전체 훈련 세트(배치 경사하강법)이나 하나의 샘플(확률적 경사 하강법)을 기반으로 기울기를 계산하지 않고, 미니 배치라고 부르는 임의의 샘플 세트를 기반으로 기울기를 계산함.
- 1개의 배치에 임의의 학습 데이터 여러 개가 들어감
- 배치 경사하강법보다 효율적이고, 확률적 경사하강법 보다 노이즈가 적다.
- 행렬 연산에 최적화된 하드웨어(GPU를 사용하는 경우)에서 성능이 향상됨.
'머신러닝 및 딥러닝 > 머신러닝' 카테고리의 다른 글
| 머신러닝 모델 최적화 - 과적합 (0) | 2023.02.08 |
|---|---|
| 다항회귀이론( + 사이킷런 transformer) (0) | 2023.02.08 |
| 경사하강법 이론2(+ Feature Scaling) (0) | 2023.02.08 |
| 다중선형회귀 이론 (0) | 2023.02.07 |
| 선형회귀 이론 (1) | 2023.02.07 |
