분류(classification)의 개요
학습 데이터로 주어진 피처와 레이블(결정값, 클래스값)을 머신러닝 알고리즘으로 학습해 모델을 생성하고, 이렇게 생성된 모델
에 새로운 데이터값이 주어졌을때 미지의 레이블을 예측하는 것.
기존 데이터가 어떤 레이블에 속하는지 패턴을 알고리즘으로 학습 -> 새롭게 관측된 데이터의 레이블을 판별
분류 알고리즘
- 나이브베이즈 - 베이즈 통계와 생성 모델
- 독립 변수와 종속 변수와 선형 관계성에 기반에 로지스틱 회귀
- 데이터 균일도에 따른 규칙 기반 결정 트리
- 개별 클래스 간의 최대 분류 마진을 효과적으로 찾아주는 SVM
- 근접 거리를 기준으로 하는 최소 근접 알고리즘(KNN nearest Neighbor)
- 심층 연결 기반의 신경망(딥러닝)
- 서로 다른(같은) 머신 러닝 알고리즘을 결합한 앙상블
앙상블
- 배깅 - 랜덤 포레스트: 뛰어난 예측 성능, 빠른 시간, 유연성
- 부스팅 -
1) 그래디언트 부스팅 - 뛰어난 예측성능, 단, 수행시간 길다.최적화 모델 튜닝 어렵다.
2) XGBoost, LightGBM - 예측 성능은 높이고 수행시간은 단축. 정형 데이터 분류 영역에서 가장 활용도가 높다. - 스태킹 - 앙상블의 앙상블
앙상블 - 분류에서 가장 각광을 받는 방법 중 하나, 정형 데이터의 예측 분석 영역(cf. 딥러닝 - 이미지, 영상, 음성, NLP 영역)
앙상블의 기본 알고리즘- 결정 트리
결정트리
- 직관적으로 이해하기 쉬운 머신러닝 알고리즘
- 종속 변수가 범주형일 경우, 수치형일 경우 모두 사용할 수 있는 지도학습 방법론이다
- 결과에 대한 해석이 용이하여 정책 의사결정에 폭넓게 사용되는 방법론이다.
- 주어진 설명 변수(연속형, 범주형)를 활용해 의사결정 규칙(rule)을 자동으로 찾아내 트리 기반의 분류 규칙을 생성한다.
- 결정트리 알고리즘은 데이터나 오차 등에 대한 어떠한 가정도 필요 없는 비모수 방법(non-parametricmethod)으로 유연하게 사용할 수 있다.
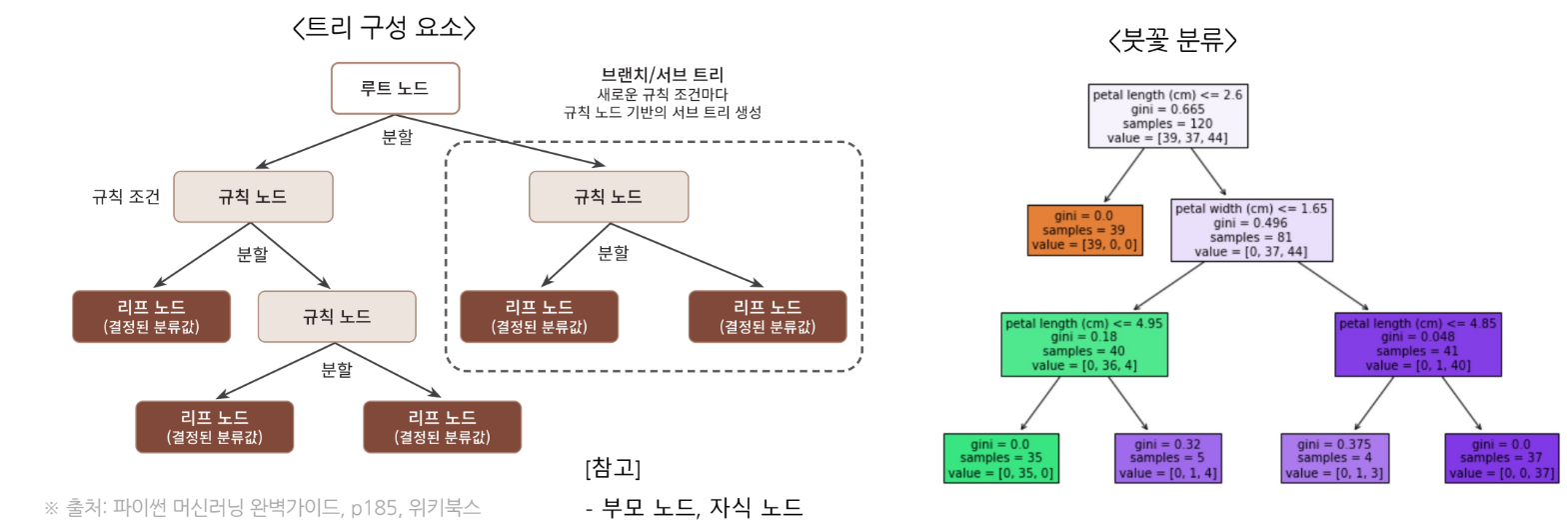
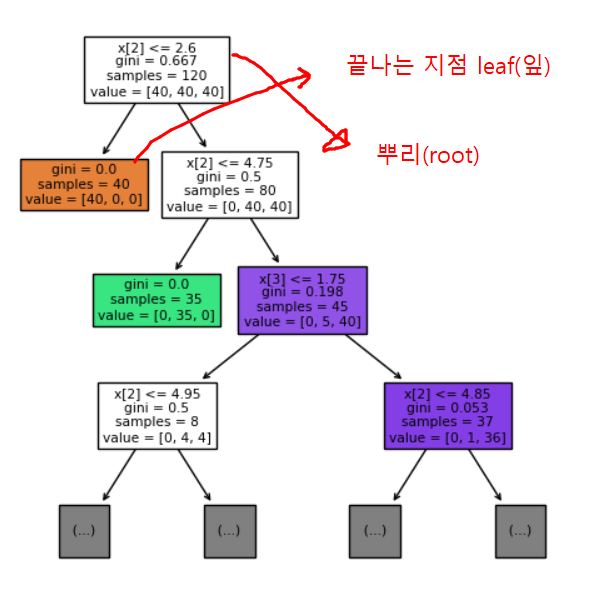
트리의 분할원리
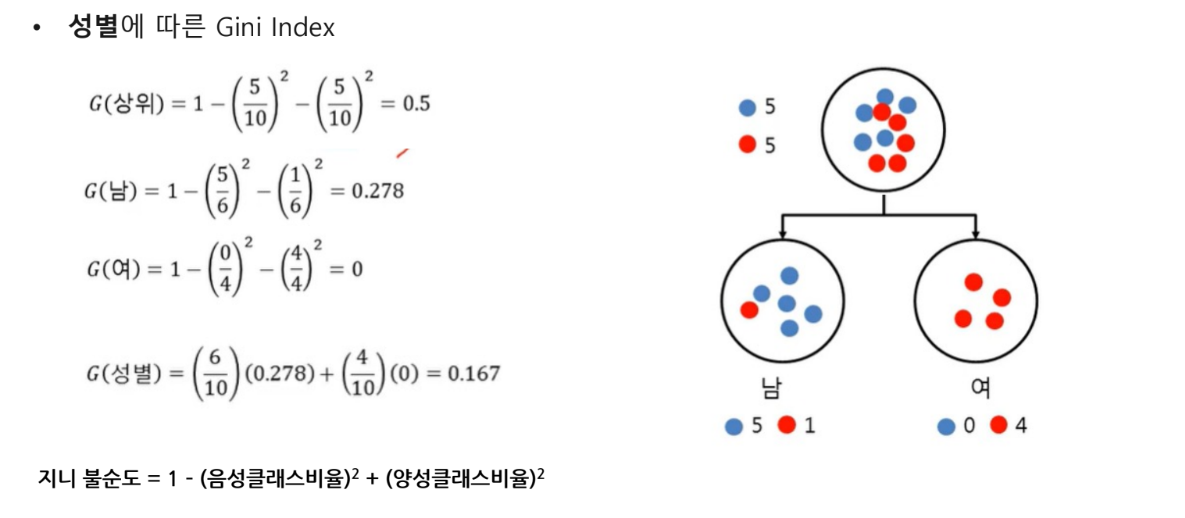
순수도(Purity) 또는 불순도(Inpurity) 측정
- 순수도 또는 불순도에 의해 측정
- 순수도(Purity) : 특정 범주의 개체들이 포함된 정도
- 불순도(Impurity) : 얼마나 다양한 개체들이 포함되어 있는가 계산
- 분할 속성의 선택
- 부모 마디의 순수도에 비해서 자식 마디의 순수도가 증가하도록 자식 마디를 형성
- 예) 그룹0과 그룹1의 비율이 45%와 55%인 마디는 각 그룹의 비율이 90%와 10%인 마디에 비해 순수도가 낮음(불순도가 높음)
- 마지막에 도달한 노드의 클래스 비율을 보고 예측을 만듦.
- 단, 결정트리는 끝까지(greedy) 분할을 하기 때문에 과적합이 생기기 쉽다. (가지치기 또는 과적합 개선 처리가 필요)
- 가치지기
- 트리의 최대깊이 지정(max_depth)
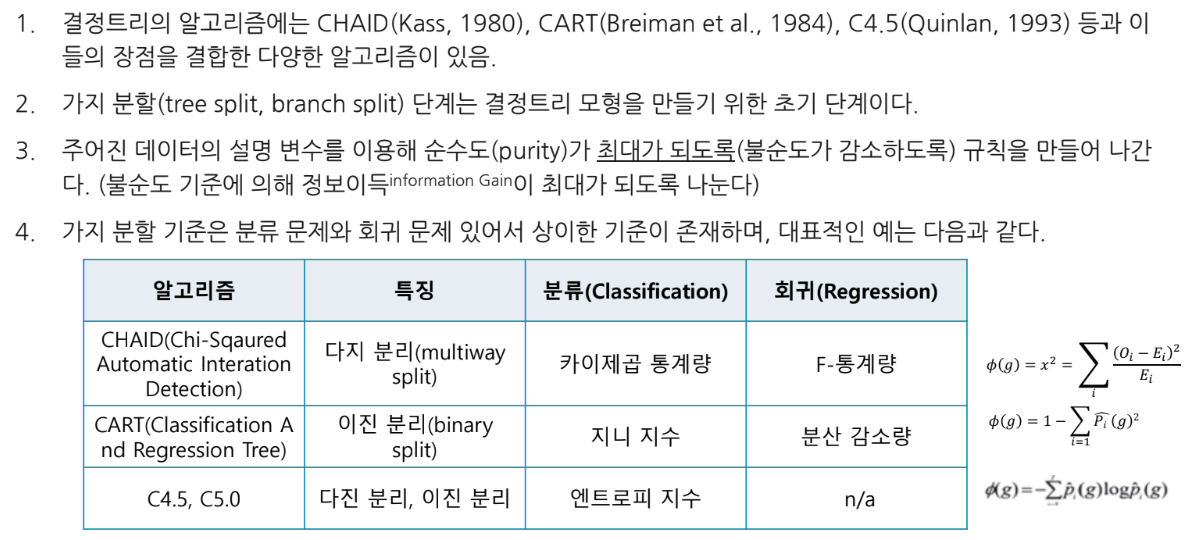
결정트리 분류 기준- CART
- CART(Classification And Regression Tree)
- Breiman 등이 개발
- 분류 및 회귀 양쪽 모두 사용 가능
- 불순도 알고리즘: Gini 지수(Gini Index) - 불확실성의 증감으로 판정
- 분리: 2지 분리(Binary Split)
- 가지치기(교차 타당도) : 학습 데이터를 이용하여 나무를 성장시키고 검증용 데이터를 이용하여 가지치기
- 2번 복원추출을 했을 때 나올 수 있는 확률
정보 엔트로피

지니불순도 vs 엔트로피
실제로는 큰 차이가 없이 둘 다 비슷한 트리를 만듦
지니 불순도가 조금 더 계산이 빠르기 때문에 기본값으로 좋음
그러나 다른 트리가 만들어지는 경우 지니 불순도가 가장 빈도 높은 클래스를 한쪽 가지(branch)로 고립시키는
경향이 있는 반면 엔트로피는 조금 더 균형 잡힌 트리를 만듦
'머신러닝 및 딥러닝 > 머신러닝' 카테고리의 다른 글
| Gradient Boosting(GBM), LGBM, XGBOOST (0) | 2023.02.13 |
|---|---|
| 앙상블 이론 (0) | 2023.02.13 |
| 로지스틱 회귀 이론(분류), 분류 성능평가지표 (0) | 2023.02.09 |
| 규제가 있는 선형회귀 - 라쏘, 릿지, 엘라스틱넷 회귀 (0) | 2023.02.09 |
| 머신러닝 모델 최적화 - 편향,분산 트레이드오프 / 교차 검증 (0) | 2023.02.09 |
분류(classification)의 개요
학습 데이터로 주어진 피처와 레이블(결정값, 클래스값)을 머신러닝 알고리즘으로 학습해 모델을 생성하고, 이렇게 생성된 모델
에 새로운 데이터값이 주어졌을때 미지의 레이블을 예측하는 것.
기존 데이터가 어떤 레이블에 속하는지 패턴을 알고리즘으로 학습 -> 새롭게 관측된 데이터의 레이블을 판별
분류 알고리즘
- 나이브베이즈 - 베이즈 통계와 생성 모델
- 독립 변수와 종속 변수와 선형 관계성에 기반에 로지스틱 회귀
- 데이터 균일도에 따른 규칙 기반 결정 트리
- 개별 클래스 간의 최대 분류 마진을 효과적으로 찾아주는 SVM
- 근접 거리를 기준으로 하는 최소 근접 알고리즘(KNN nearest Neighbor)
- 심층 연결 기반의 신경망(딥러닝)
- 서로 다른(같은) 머신 러닝 알고리즘을 결합한 앙상블
앙상블
- 배깅 - 랜덤 포레스트: 뛰어난 예측 성능, 빠른 시간, 유연성
- 부스팅 -
1) 그래디언트 부스팅 - 뛰어난 예측성능, 단, 수행시간 길다.최적화 모델 튜닝 어렵다.
2) XGBoost, LightGBM - 예측 성능은 높이고 수행시간은 단축. 정형 데이터 분류 영역에서 가장 활용도가 높다. - 스태킹 - 앙상블의 앙상블
앙상블 - 분류에서 가장 각광을 받는 방법 중 하나, 정형 데이터의 예측 분석 영역(cf. 딥러닝 - 이미지, 영상, 음성, NLP 영역)
앙상블의 기본 알고리즘- 결정 트리
결정트리
- 직관적으로 이해하기 쉬운 머신러닝 알고리즘
- 종속 변수가 범주형일 경우, 수치형일 경우 모두 사용할 수 있는 지도학습 방법론이다
- 결과에 대한 해석이 용이하여 정책 의사결정에 폭넓게 사용되는 방법론이다.
- 주어진 설명 변수(연속형, 범주형)를 활용해 의사결정 규칙(rule)을 자동으로 찾아내 트리 기반의 분류 규칙을 생성한다.
- 결정트리 알고리즘은 데이터나 오차 등에 대한 어떠한 가정도 필요 없는 비모수 방법(non-parametricmethod)으로 유연하게 사용할 수 있다.


트리의 분할원리

순수도(Purity) 또는 불순도(Inpurity) 측정
- 순수도 또는 불순도에 의해 측정
- 순수도(Purity) : 특정 범주의 개체들이 포함된 정도
- 불순도(Impurity) : 얼마나 다양한 개체들이 포함되어 있는가 계산
- 분할 속성의 선택
- 부모 마디의 순수도에 비해서 자식 마디의 순수도가 증가하도록 자식 마디를 형성
- 예) 그룹0과 그룹1의 비율이 45%와 55%인 마디는 각 그룹의 비율이 90%와 10%인 마디에 비해 순수도가 낮음(불순도가 높음)
- 마지막에 도달한 노드의 클래스 비율을 보고 예측을 만듦.
- 단, 결정트리는 끝까지(greedy) 분할을 하기 때문에 과적합이 생기기 쉽다. (가지치기 또는 과적합 개선 처리가 필요)
- 가치지기
- 트리의 최대깊이 지정(max_depth)
결정트리 분류 기준- CART
- CART(Classification And Regression Tree)
- Breiman 등이 개발
- 분류 및 회귀 양쪽 모두 사용 가능
- 불순도 알고리즘: Gini 지수(Gini Index) - 불확실성의 증감으로 판정
- 분리: 2지 분리(Binary Split)
- 가지치기(교차 타당도) : 학습 데이터를 이용하여 나무를 성장시키고 검증용 데이터를 이용하여 가지치기
- 2번 복원추출을 했을 때 나올 수 있는 확률

정보 엔트로피

지니불순도 vs 엔트로피
실제로는 큰 차이가 없이 둘 다 비슷한 트리를 만듦
지니 불순도가 조금 더 계산이 빠르기 때문에 기본값으로 좋음
그러나 다른 트리가 만들어지는 경우 지니 불순도가 가장 빈도 높은 클래스를 한쪽 가지(branch)로 고립시키는
경향이 있는 반면 엔트로피는 조금 더 균형 잡힌 트리를 만듦
'머신러닝 및 딥러닝 > 머신러닝' 카테고리의 다른 글
| Gradient Boosting(GBM), LGBM, XGBOOST (0) | 2023.02.13 |
|---|---|
| 앙상블 이론 (0) | 2023.02.13 |
| 로지스틱 회귀 이론(분류), 분류 성능평가지표 (0) | 2023.02.09 |
| 규제가 있는 선형회귀 - 라쏘, 릿지, 엘라스틱넷 회귀 (0) | 2023.02.09 |
| 머신러닝 모델 최적화 - 편향,분산 트레이드오프 / 교차 검증 (0) | 2023.02.09 |
