군집 평가(Cluster Evaluation)
- 실루엣 분석(sillhouette analysis)
- 각 군집 간의 거리가 얼마나 효율적으로 분리되었는지 나타냄
- 클러스터 내 데이터들이 얼마나 조밀하게 모여있는지 측정하는 도구
- 다른 군집과 거리는 떨어져있고, 동일 군집끼리의 데이터는 잘 뭉쳐있어야함
- 군집화가 잘 이루어질수록, 개별 군집은 비슷한 정도의 여유 공간을 가지고 떨어져 있음.
- 실루엣 계수(Silhouetta coefficient) : 개별 데이터가 가지는 군집화 지표
- 해당 데이터가 같은 군집 내의 데이터와 얼마나 가깝게 군집 되어있고, 다른 군집에 있는 데이터와는 얼마나 멀리 분리 되어있는지 나타내는 지표
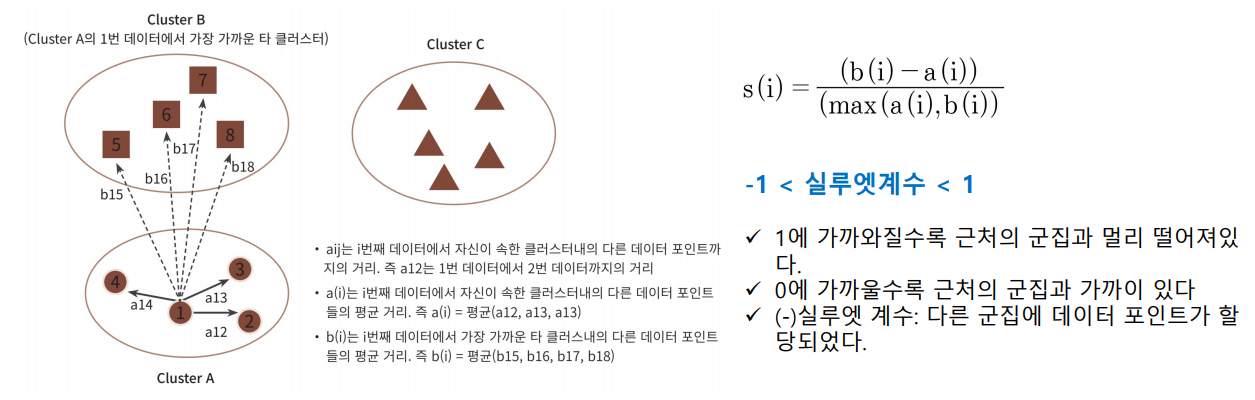
군집 간 비교시, 가장 가까운 군집만 비교해서, 그림에서 군집 C는 무시한다.
군집화 결과 판단 기준
- 전체 실루엣 계수의 평균값이 0~1 사이 값을 가지며, 1에 가까울수록 좋다.
- 개별 군집의 평균값 차이가 작아야한다.
- 개별 군집의 실루엣 계수 평균값이 전체 실루엣 계수의 평균값이 크게 벗어나지 않는 것이 중요하다.
- 만약 전체 실루엣 계수의 평균값은 높지만, 특정 군집의 실루엣계수 평균값만 유난히 높고 다른 군집들의 실루엣 계수 평균값만 낮으면 좋은 군집이라고 할 수 없다.
군집 개수를 정하는 방법
- 엘보우 기법
- 실루엣 계수
- 덴드로그램
DBSCAN 군집화 알고리즘(Density-Based Spatial Clustering of Applications with Noise)
- 밀도 기반 군집화의 대표적 알고리즘(특정 공간 내의 데이터 밀도 차이를 기반으로 함)
- K-Means와 같이 원형 클러스터를 가정하지 않음
DBSCAN의 장점
- 간단하고 직관적인 알고리즘
- 데이터의 분포가 기하학적이 복잡한 데이터셋에도 효과적인 군집화 가능
- 사전에 클러스터의 개수를 지정하지 않고, 분석 결과로 클러스트의 개수가 정해짐
- 데이터가 위치하고 있는 공간 밀집도 기준으로 클러스터를 구분
- 핵심(코어) 포인트(Core Point) : 자기를 중심으로 반지름 R의 공간에 최소 M개의 포인트가 존재하는 점
- 아웃 포인트(Neighbor Point) : 핵심 포인트 주변 영역(R) 내에 위치한 타 데이터
- 경계 포인트(Border point) : 코어포인트는 아니지만 반지름 R 안에 다른 코어포인트가 있는 경우
- Noise(outlier) : 코어 포인트도 아니고 경계포인트도 아닌 점
DBSCAN 방식의 군집화를 결정하는 파라미터
입실론(epsilon 주변 영역) - 핵심 포인트로부터의 반경
최소 데이터 개수(min points) - 입실론 주변 영역에 포함되는 타 데이터의 개수

덴드로그램 - 계층적 군집 구성 방법
- 계층적 클러스터링은 각 레코드 자체를 개별 군집으로 설정하여 시작하고, 가장 가까운 클러스터를 결합해나가는 작업을 반복함(상향식, 병합 군집)
- 특이점이나 비정상적인 그룹이나 레코드를 발견하는데 민감함
- 직관적인 시각화 가능(덴드로그램, 해석이 수월하다)
- 상대적으로 데이터 크기가 작은 문제에 주로 적용되며, 수백만 개의 대규모 레코드에는 적용할 수 없다(유연성 비용)
- 측정 비용
- 레코드간의 거리, 군집간의 유사도
- 트리의 잎 : 각각의 표본(레코드)
- 트리의 가지 길이 : 해당 클러스터 간의 차이 정도
- 클러스터의 수를 미리 지정할 필요가 없다.
- 위 아래로 움직이는 수평선을 통해 클러스터 식별

평균 이동(Mean Shift) 군집화 알고리즘
GMM 군집화 알고리즘
최적의 군집 알고리즘 선택
실전에서는 실전에서는 어떤 군집 알고리즘이 주어진 데이터셋에서 최상일지 확실하지 않음
특히 시각화하기 어렵거나 불가능한 고차원 데이터셋일 때 그러함
성공적인 군집은 알고리즘이나 하이퍼파라미터에만 의존하는 것이 아니라는 점도 강조하고 싶음
오히려 적절한 거리 지표를 선택하고 실험 환경을 구성하는 데 도움을 줄 수 있는 도메인(domain) 지식이 더 중요할 수 있음
차원의 저주를 고려하면 군집을 수행하기 전에 차원 축소 기법을 적용하는 것이 일반적임
비지도 학습용 데이터셋을 위한 차원 축소 기법에는 주성분 분석과 RBF 커널 주성분 분석이 해당
데이터셋을 2차원 부분 공간으로 압축하면 2차원 산점도에서 클러스터를 시각화하고 레이블을 할당할 수 있음
특히 결과를 평가할 때 도움이 됨
요약
- 세 종류의 군집 알고리즘을 먼저 익힐 것
- 프로토타입 기반 방식인 k-Means
- k-평균은 지정된 클러스터 센트로이드 개수에 맞게 샘플을 원형의 클러스터로 묶음
- 군집은 비지도 학습 방법이기 때문에 모델 성능을 평가하기 위해 사용할 정답 레이블이 없음
- 군집 품질을 평가하기 위해서는 엘보우 방법이나 실루엣 분석처럼 알고리즘 자체의 성능 지표를 사용
- 병합 계층 군집 - 사전에 클러스터 개수를 지정할 필요가 없음
- 군집 결과는 덴드로그램으로 시각화할 수 있어 결과를 이해하는 데 도움이 됨
- DBSCAN - 밀집된 지역을 기반으로 샘플을 모으는 알고리즘이며, 이상치를 구분하고 원형이 아닌 클러스터를 찾아낼 수 있음
'머신러닝 및 딥러닝 > 머신러닝' 카테고리의 다른 글
| 오버샘플링 vs 언더샘플링 (0) | 2023.02.14 |
|---|---|
| 스태킹 앙상블(Stacking Ensemble, 블렌딩) (0) | 2023.02.14 |
| Gradient Boosting(GBM), LGBM, XGBOOST (0) | 2023.02.13 |
| 앙상블 이론 (0) | 2023.02.13 |
| 결정트리 이론 (0) | 2023.02.10 |
